
I suggest a number of simple (single compositions) first and then a few longer ones and maybe one or two “monsters” just for fun once they get the idea. The students will need some practice on using the Chain Rule. Since this is true, it must go through the values three times as fast thus, its derivative (it’s rate of change) must be three times the derivative of the sine. (That is its period is one-third of the period of. This function takes on all the values of in order in one-third the time. The closest I could come up with is this: Consider. I have been looking for a way to illustrate the Chain Rule graphically, but to no avail.
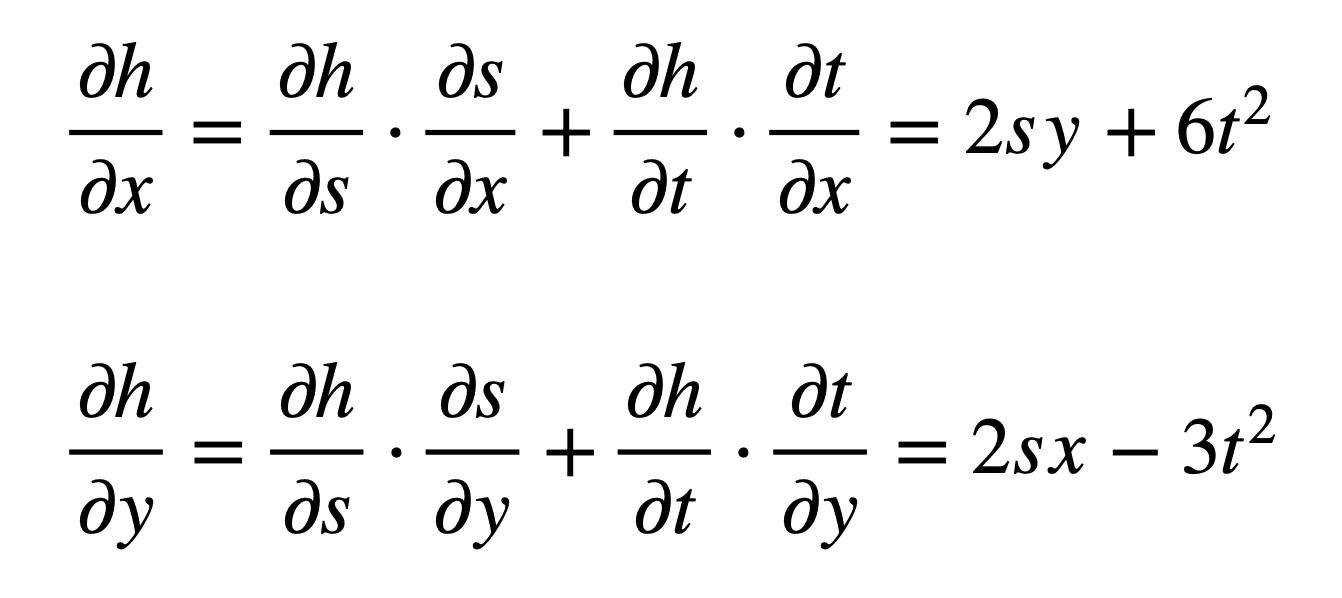
The cartoon below is from Courtney Gibbons’ great collection of math cartoons ( ) may help you kids remember this: This can be extended to compositions of more than two functions: To differentiate you (1) use the power rule to differentiate the 53 power of whatever is inside, this gives, the (2) differentiate the which give 2 and multiply the results. To evaluate the expression above you (1) evaluate the expression inside the parentheses and the (2) raise that result to the 53 power. It is done in the exact opposite order than the procedure for evaluating expression. The differentiation is done from the outside, working inward. Students must get good at recognizing compositions.

The Chain Rule is used for differentiating compositions. Then our original expression becomes a composition of functions.

They will see the need for a short cut at once. They will try the same approach with and then you can hit them with. Most students will expand the binomial to get and differentiate the result to get. You can start with an example such as finding the derivative of. Except for the simplest functions, a procedure known as the Chain Rule is very helpful and often necessary to find derivatives.


 0 kommentar(er)
0 kommentar(er)
